| Validierung von Berechnungsalgorithmen für zweidimensionale Wärmebrückenprobleme |
Die EN 10211:2007 definiert eine Prozedur für die Validierung von Software für Wärmebrückenberechnungen. Der Arbeitsablauf
ist in Anhang A für 2 verschiedene zweidimensionale Simulationsfälle gegliedert. Wie unten beschrieben kann die Software DELPHIN
als Programm für zweidimensionale, instationäre Wärme- und Feuchte Simulationen für die Berechnung der Fälle verwendet werden.
Wenn DELPHIN für stationäre Zustandsberechnungen benutzen werden soll, werden konstante Randbedingungen aufgeprägt. Die Simulation
sollte solange laufen, bis Veränderungen resultierend von den Anfangsbedingungen verschwinden und konstante Prozesse eintreten.
Daher hat die Auswahl der Anfangsbedingungen Auswirkungen auf die Simulationsdauer. | |
Wir empfehlen, mit einer kurzen Simulationszeit von wenigen Stunden bis 2 Tagen zu beginnen und dabei stündliche Ausgabewerte zu verwenden.
Wenn die angezeigten Variablen sich immer noch verändern, können wir die Simulationszeit mit einem Faktor von 2 oder 3 verlängern
(abhängig von dem Ausmaß der Abweichung) die Simulation fortsetzen. Im Normalfall erreichen sogar komplexe Konstruktionen binnen
weniger Simulations-Tage den stationären Zustand.
In den Simulationen für die EN 10211:2007 Validierungen benötigen wir manchmal Simulationszeiten von über 40 Tagen (das sagt auch schon
so einiges über die Warscheinlichkeit aus, dass eine stationäre Situation im wahren Leben überhaupt erreicht werden kann).
|
| Validierungsfall 1 |
Dieser Fall einer Fläche benutzt die Symmetrie des Bauteils in der Berechnung. Die Ausgaben sollten in definierten Gitterpunkten bestimmt werden.
Wir benutzen in DELPHIN einen Modellierungstrick um das Gitter zu generieren. Wir definieren zwei Materialien mit den selben Beschaffenheiten,
aber mit unterschiedlichen Namen. Wir erstellen ein Schachbrettmuster mit diesen Materialien. Jetzt können wir den eingebauten Gittergenerator verwenden,
legen das Minimum der Elementdicke und den Ausdehnungsfaktor fest und generieren das benötigte Gitter.
Das generierte Gitter wird in der Grafik auf der rechten Seite dargestellt.
| |  Das ist das generierte Gitter mit einer Elementdicke von 1mm, einen Ausdehnungsfaktor von 1.476 und einer Elemtanzahl von 15488.
Das ist das generierte Gitter mit einer Elementdicke von 1mm, einen Ausdehnungsfaktor von 1.476 und einer Elemtanzahl von 15488.
|
|
Validierungsergebnisse und Projekt
Das fertige Projekt, welches wir für die Validierung benutzten, kann über den untenstehenden Link heruntergeladen werden. Es wurde in den Versionen 5.6.4 und 5.6.5 getestet.
Das nächste DELPHIN hat die 2 Fälle schon als Beispiele integriert.
EN_ISO_10211_2007_Case1.dpj
(Rechtsklick auf den Link zum Speichern)
Die berechneten Ergebnisse werden in den nachfolgenden Tabellen mit den Originalwerten und den entstandenen Abweichungen dargestellt.
Alle Abweichungen befinden sich unter des Grenzwerts von 0,1 Kelvin.
Die erste Tabelle beinhaltet die mit dem Simulationsprogramm DELPHIN berechneten Ergebnisse. Die Werte in Klammern sind
Referenzwerte zum Vergleich.
| |
9.659 (9.7) 13.385 (13.4) 14.736 (14.7) 15.093 (15.1)
5.249 (5.3) 8.643 (8.6) 10.320 (10.3) 10.815 (10.8)
3.186 (3.2) 5.610 (5.6) 7.017 (7.0) 7.468 (7.5)
2.012 (2.0) 3.641 (3.6) 4.660 (4.7) 5.002 (5.0)
1.261 (1.3) 2.308 (2.3) 2.987 (3.0) 3.219 (3.2)
0.739 (0.7) 1.359 (1.4) 1.767 (1.8) 1.908 (1.9)
0.341 (0.3) 0.629 (0.6) 0.819 (0.8) 0.886 (0.9)
Die folgende Tabelle stellt die Abweichungen der Berechnungen von den gegebenen Werten dar.
0.04 0.02 0.04 0.01
0.05 0.04 0.02 0.01
0.01 0.01 0.02 0.03
0.01 0.04 0.04 0.00
0.04 0.01 0.01 0.02
0.04 0.04 0.03 0.01
0.04 0.03 0.02 0.01
|
|
Gittersensitivitätsstudie
Gittersensitivitätsstudien werden erstellt, um numerische Fehler, welche durch Art und Form des Berechnungsgitters
in die Ergebnisse einfließen, quantitativ abschätzen zu können. So können die Auswirkungen verschiedener
Gittergenerierungsparameter untersucht werden, die maßgeblich die Dichte des numerischen Gitters beeinflussen.
In unseren 2 Fällen untersuchen wir, welche Auswirkungen eine Veränderung des Gitters auf die berechneten
Temperaturverteilungen im Bauteil hat. Dafür verändern wir die minimale Elementdicke und den Stretchfaktor, und
somit auch die Elementanzahl. Das sind die ausschlaggebenden Faktoren, um das Bauteilgitter entscheidend zu
beeinflussen und die Auswirkungen zu untersuchen.
| |
Einer der variierten Parameter ist der Stretchfaktor. Er gibt das Größenverhältnis zweier benachbarter Elemente und
damit die Ausdehnung des Gitters an. Der andere beschreibt die minimale Dicke der Elemente am Rand, bzw. an
Materialgrenzen. Durch Angabe der beiden Parameter berechnet sich die maximale Elementdicke automatisch,
sofern keine obere Grenze festgelegt wird.
In den ersten beiden Diagrammen wird jeweils einer dieser beiden Parameter variiert, während der andere gleich bleibt.
Im dritten Fall wird untersucht, inwieweit sich die Berechnungsergebnisse verbessern, wenn die Veränderung beider Parameter zu einem stetig feineren Gitter führt.
Auf der Abszissenachse der Diagramme werden die Elementanzahlen, die minimale Dicke der Elemente bzw. der Stretchfaktor
der verschiedenen Fälle dargestellt. Auf der Ordinate wird die Differenz der berechneten und der in der Norm gegebenen
Temperaturen angezeigt. Aus den 28 berechneten Punkten des Bauteils wurden die 6 prägnantesten Punkte
ausgewählt und in den Diagrammen angezeigt.
|
Diagramm 1: veränderte Stretchfaktoren
Der Stretchfaktor variiert in diesen Diagramm von 1,15 bis 1,51. Die minimale Elementbreite wurde dabei stets auf 1 mm gesetzt.
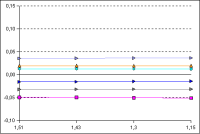
(Auf das Diagram zum Vergrößern klicken)
Durch die Geradlinigkeit der Linien zeigt sich, dass der Stretchfaktor keinen wesentlichen Einfluss auf die Ergebnisse hat.
| |
Diagramm 2: veränderte minimale Elementdicke
Der Parameter für die minimale Breite/Höhe der Gitterelemente am Rand wurde im Bereich von 1 mm bis 10 mm verändert,
dabei blieb der Stretchfaktor konstant bei 1,51.
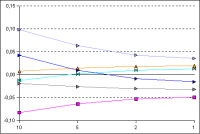
(Auf das Diagram zum Vergrößern klicken)
Es zeigt sich, dass die Elementgröße am Rand bzw. an Materialgrenzen einen wesentlichen Einfluss auf die Ergebnisse hat.
Insbesondere sieht man, dass bei größeren Randelementen und damit einer geringerer Elementanzahl die berechneten Temperaturen
stärker von den gegebenen Temperaturen abweichen. Werden die Gitterelemente am Rand verkleinert (kleinere minimale Elementdicke),
werden die Gitter feiner, und die Abweichungen nehmen ab.
Ab einer minimalen Elementdicke von 1 mm bewirkt eine weitere Verkleinerung der Randelemente in diesem Testfall nur noch eine
geringfügige Verbesserung der Resultate. Man kann also davon ausgehen, dass die Ergebnisse ausreichend genau bestimmt wurden.
|
|
Diagramm 3: allgemeine Verfeinerung des Gitters
Der Stretchfaktor wird hierbei von 1,51 beim gröbsten Gitter zu 1,21 beim feinsten Gitter verändert. Gleichzeitig wird die
minimale Elementbreite von 10 mm auf 1 mm verringert.
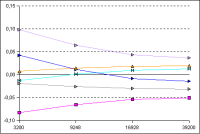
(Auf das Diagram zum Vergrößern klicken)
| |
Die folgende Tabelle zeigt die betrachteten Fälle, und die jeweilige Anzahl an Elementen im Berechnungsgitter.
Fall Elemente min stretch
I 3200 10 1,51
II 9248 5 1,3
III 16928 2 1,3
IV 39200 1 1,21
Die Ergebnisse sind mit den im Diagramm für die minimale Elementdicke gezeigten nahezu identisch. Es ist demnach also
wichtiger, mit einer kleinen Elementdicke am Rand zu rechnen, als optisch feinere Gitter durch kleine
Stretchfaktoren zu erzeugen. Letzteres führt zu mehr Elementen und längeren Berechnungszeiten,
aber kaum gesteigerter Genauigkeit.
Bei instationären Simulationen, vor allem bei Berücksichtigung von Feuchtetransport, können jedoch auch im Inneren des Bauteils starke
Gradienten auftreten. Ein Beispiel hierfür wäre eine Simulation eines Wasseraufsaugversuchs. Hier wird der Stretchfaktor wieder wichtig!
|
| Validierungsfall 2 |
Dieser Validierungsfall stellt die Berechnung eines zweidimensionalen Details dar, welches aus Beton, Holz, Wärmedämmung und
Aluminiumblech besteht.
Die Konstruktion wurde wie im rechten Bild zu sehen modelliert. Üblicherweise erfordern dünne Metallbleche eine sehr feines Gitter um
und nahe den Blechlagen. Ebenso werden schmale Elemente nahe der Oberfläche zur Erfassung des Wärmestromes benötigt.
Außerdem führen die großen Unterschiede zwischen der Wärmeleitfähigkeit der Materialien zu längeren Berechnungenszeiten.
Trotzdem ist die Berechnung auch bei einem sehr detaillierten Gitter binnen 3 Minuten an einen normalen PC abgeschlossen.
| |
Die nächste Grafik zeigt das Simulationsmodell ohne Diskretisierung.

Nun wird eine grobe Diskretisierung für den zweiten Fall mit nur 6460 Elementen dargestellt.
|
|
Validierungsergebnisse und Projekt
Das fertige Projekt welches wir für die Validierung benutzt haben, kann über den untenstehenden Link heruntergeladen werden.
Es wurde mit den DELPHIN Versionen 5.6.4 und 5.6.5 getestet. Die nächste DELPHIN Version hat die 2 Fälle schon als Beispiele integriert.
EN_ISO_10211_2007_Case2.dpj
(Rechtsklick auf den Link zum speichern)
Die berechneten Ergebnisse werden in den nachfolgenden Tabellen mit den Originalwerten und den Abweichungen dargestellt.
Alle Abweichungen befinden sich unter dem Wert von 0,1 Kelvin.
| |
Die erste Tabelle beinhaltet die mit dem Simulationsprogramm DELPHIN berechneten Ergebnisse.
Die Werte in Klammern sind Referenzwerte zum Vergleich.
A: 7.125 (7.1) 0.025
B: 0.763 (0.8) 0.037
C: 7.967 (7.9) 0.067
D: 6.331 (6.3) 0.031
E: 0.829 (0.8) 0.029
F: 16.384 (16.4) 0.016
G: 16.249 (16.3) 0.051
H: 16.747 (16.8) 0.053
I: 18.328 (18.3) 0.028
Gesamtwärmestrom: 9.534 (9.5) W/m
Wärmestromdifferenz: 0.034 W/m
|
|
Gittersensibilitätsstudie
In diesen Fall wurde ebenfalls eine Gittersensitivitätsstudie durchgeführt. Die Ergebnisse sind Beispielhaft für ausgewählte Punkte dargestellt. Für jede Gittervariation wurde eine Berechnung durchgeführt. Variationsstudien haben gezeigt, dass auch hier der Stretchfaktor keinen wesentlichen Einfluss auf die Ergebnisse hat. Somit werden in der folgenden Diskussion lediglich die minimalen Elementdicken am Rand betrachtet, und alle Gittervarianten werden mit einem Stretchfaktor von 1,51 erzeugt.
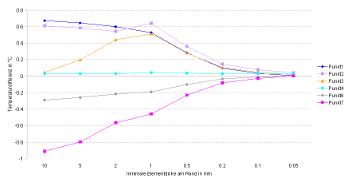
(Auf das Diagram zum Vergrößern klicken)
| |
Auf der Abzissenachse ist die minimale Elementdicke in mm angetragen und die Ordinate stellt die Temperaturdifferenzen (zu den Referenztemperaturen) an ausgewählten Sensorpunkten in K dar. Die minimale Elementdicke spielt bei der Gittergenerierung eine ganz wesentliche Rolle, da das Bauteil von einen gut Wärme leitenden Aluminiumblech durchzogen wird, und so großen Einfluss auf die Temperaturverteilung nimmt. Deshalb ist in dem Bereich, wo sich das Blech befindet, ein sehr feines Gitter zu wählen, um möglichst genaue Ergebnisse zu bekommen. Aus diesem Grund wurde die minimale Elementdicke am Rand bzw. an Materialschichtgrenzen zwischen 10 mm und 0,05 mm variiert. Wie man in dem Diagramm unschwer erkennen kann, verändern sich die Ergebnisse unterhalb von 0,2 mm nicht mehr sehr stark, wobei von 10 mm bis 0,5 mm für einzelne Punkte zum Teil drastische Unterschiede in den berechneten Temperaturen auftreten.
Der starke Einfluss der Elementdicke am Rand bzw. an Bauteilgrenzen auf die Genauigkeit des Ergebnisses lässt sich mit der numerischen Umsetzung
der Randbedingung erklären. Bei der Kontrollvolumenmethode, welche in DELPHIN Anwendung findet, wird je Element ein einziger Zustand definiert. Dadurch wird keine Verteilung der Erhaltungsgrößen innerhalb des Elements beschrieben. Die Temperatur am Rand des Elements wird also als genausogroß angenommen, wie am Mittelpunkt des Elements. Dieses führt bei starken Temperaturgradienten am Rand zu einem Fehler, welcher direkt proportional zur Elementgröße am Rand ist. Daher sollten in Bereichen starker Temperaturgradienten stets kleine Gitterelemente verwendet werden.
|
| | |